Musical notes are related to each other through ratios of frequencies. Our ears have a roughly logarithmic scale. Therefore, pairs of notes which have similar ratios, sound alike in arrangement. As an example, in the below clip, I am playing a C₄ and F₄# first and F₄# and C₅ later (first on a flute and then on a piano). The frequencies are 261.63 Hz (C₄),  369.94 Hz (F₄#) and 523.25 Hz (C₅). Ratios are 1 : 1.414 (√2) in both the cases. Note that the type of the instrument hardly matters in discerning the arrangement. 

Real instruments don’t produce pure tones, there are a lot of harmonics and each harmonic fades at a different rate. This set of characteristics of a particular instrument is called timbre. Timbre makes instruments sound different from one another although they ma be playing the same note.

Ears recognize tones with a frequency ratio of two to be in harmony with each other. For example, C₄ (261.63 Hz) and C₅ (523.25 Hz) are basically the same note but C₅ has twice the frequency as C₄. Therefore, a musical scale extends from one note to the next note that is twice the frequency.  Within a scale, most modern musical traditions have a maximum of 12 notes. 

Just Intonation vs Equal Temperament

Research has shown that for some not so completely understood reasons, we like notes that have a simple ratio of integers among themselves. The most basic example is that of the octave itself. That is, notes with a frequency ratio of two appear to be same note. The next smallest set of integers that can be used to form a ratio is 2 and 3. Infact, this happens to be the case with the notes C and G ( Sa and Pa in Indian notations). Therefore, C and G also happen to be the next most harmonious pair of notes. The Just Intonation temperament constructs all the notes within a scale using such simple ratios. More details here.

But, Just Intonation presents a practical problem. Singers don’t come with machine tuned voices. They would want to shift the reference scale as per their comfort and the mood of the song. If we want to shift the reference scale to another note other than C, then we have to re-tune all the notes around the new base note as per the ratio requirements. Imagine a pianist tuning all the strings every now and then to suit the singer. That would be disaster (although modern electronic instruments make this easy again). Musicians worked around this problem and approximated these ratios to the nearest numbers that formed a equal geometric progression. Such an arrangement is called Equal Temperament. For most people including several professional musicians, the difference between Just Intonation and Equal Temperament notes is not noticeable at all. Very few audiophiles and musical geniuses may be able to tell the difference between the two. More details here.Therefore, to make life easy, I will use Equal Temperament notes for all discussion from now on.

The 12 notes, the 7 major notes and scale shifting.

As mentioned previously, most modern musical traditions use a maximum of 12 notes within a scale.  Some Arabic scales use 24 notes while there are other cultures which use only 5. Nevertheless, the fundamentals of learning music remain the same. Therefore, I will continue to use the 12 notes with 7 major notes as the reference through the rest of the series. It was also discussed that these 12 notes are in a geometric progression. Therefore, it follows that the frequency ratio between each note and the next is 1:2^1/12.  Within these 12 notes, for reasons unknown (probably due to the obsession with number 7 and the cultural positive reinforcements over centuries), 7 of these notes happen to sound very natural and comforting when played consecutively. These are called the major notes in the west (Sargam in India). If we denote the step size from one note to the immediate neighbor as one, then the major notes can be represented as below –

Position	Western notation	Western numbering	Indian notation
0	C	Unison	Sa
2	D	Major Second	Re
4	E	Major Third	Ga
5	F	Major Fourth	Ma
7	G	Major Fifth	Pa
9	A	Major Sixth	Dha
11	B	Major Seventh	Ni
12	C	Octave	Sa

 

On a piano, all the major notes are white keys. The minor keys are black keys. The same applies to Indian instruments such as the harmonium. We can now place the 5 minor notes between the major notes. These are just the missing positions in the above table. i.e 1, 3, 6, 8 and 10. The complete set is given below.

Position	Western notation	Western numbering	Hindustani notation
0	C	Unison	Sa
1	C#/D♭	Minor Second	Komal Re
2	D	Major Second	Re
3	D#/E♭	Minor Third	Komal Ga
4	E	Major Third	Ga
5	F	Major Fourth	Ma
6	F#/G♭	Augmented Fourth	Tivra Ma
7	G	Major Fifth	Pa
8	G#/A♭	Minor Sixth	Komal Dha
9	A	Major Sixth	Dha
10	A#/B♭	Minor Seventh	Komal Ni
11	B	Major Seventh	Ni
12	C	Octave	Sa

 

 

 

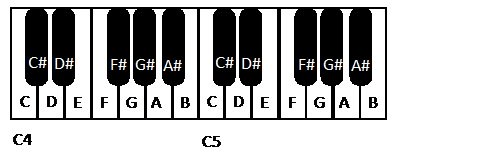
Now on, through this series, I will be referring to the western notation and the positions for ease of teaching. Positions are very useful in teaching relative arrangement of notes. If the difference in positions of two pairs of notes is the same, then the pairs sounds similar. Going back to the first example in this post, the position difference between C and F# is the same as F# and the next C. Therefore, the two pieces sounded similar.  I recommend that people use a piano/electronic synthesizer vs any other instrument for the first lessons on music as these instruments reflect the math in the music in the simplest manner. To test the theory of relative positions, you can try the following experiment – Play the two sequences below on a piano and check if they sound similar –

Case 1 : C, D, E, F, G, A , B, C (Positions are 0, 2, 4, 5, 7, 9, 11, 12)

Case 2 : C#, D#, F, F#, G#, A#, C, C# (Positions are 1, 3, 5, 6, 8, 10, 12, 13)

The two sequences played are the C and the C# scales. You can here me play it below –

Just for fun, you can try all the other 10 possibilities with different starting positions (D, D#, E and so on..) while keeping the relative positions between the successive notes same as the above examples.

Now that we have understood the theory, we can get started with the practicals. In the immediately following posts, I will elucidate the techniques for synthesizing and recognizing a small sub-set of notes which are the easiest to start with.

Other posts in this series

1. Music 101 : Why am I writing this series? (2014-April-13)
2. Music 101 : The Math (2014-June-14)
3. Music 101 : The Practical Challenges (2014-June-29)